Suites numériques
Même, si on ne veut pas toujours l'admettre, on rencontre un problème mathématique à chaque fois que l'on se confronte à des valeurs numériques mesurées (bricolage, cuisine, comptabilité, etc.) Quand on veut suivre l'évolution d'une "grandeur", on peut être amené à répéter des mesures dans le temps (toutes les années, tous les mois ou toutes les minutes). On étudie alors ce que l'on appelle une suite numérique. Et bien sûr en sciencescience au sens large : sciences physiques, sciences du vivant, étude des populations, etc., on étudie très souvent l'évolution de grandeurs numériques que ça soit la taille d'une personne, le QI moyen d'une population, la démographie d'un pays ou encore la suite des décimales de π. Cela permet notamment d'observer des tendances et de faire des prévisions. Attention toutefois à garder un esprit critique sur les prévisions à partir de données décrivant des phénomènes sociaux ou économiques ... Même si les suites numériques observées sont incontestables, les interprétations qui en découlent peuvent être plus ou moins solides. Il y a une grande différence entre une opinion personnelle et une hypothèse soumise à l'épreuve de la méthode scientifique... 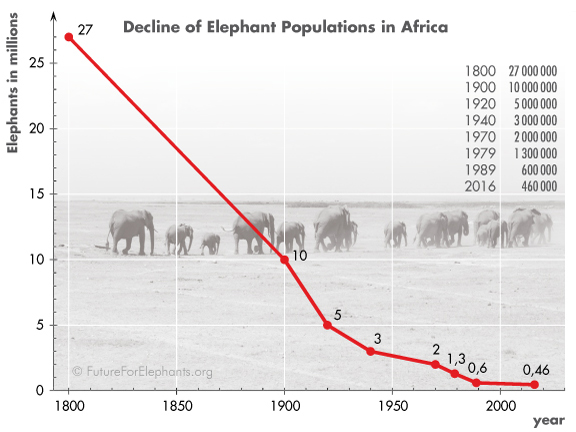Une chaîne Youtube dédiée à la pensée critique et à la methode scientifique TD fonctions affines : Quand la science prédisait des courreuses plus rapides que les courreurs... Pour refermer la parenthèse sceptique : méfiez vous des étiquettes "prouvé scientifiquement" que l'on pourrait souvent remplacer par "saupoudrage de termes scientifiques en vrac" ! saupoudrage
Une suite numérique, notée $(u_n)$ est une famille ordonnée infinie de nombres réels.
Le n-ième terme (ou terme de rang n) est noté $u_n$. Les suites numériques peuvent représenter des valeurs théoriques comme les nombres premiers, mais aussi des valeurs concrètes en évolution comme la démographie mondiale.
  • $(p_n) = (1, 2, 3, 5, 7, 11, 13, 17, 19, 23, ...)$ est la suite des nombres premiers
  • $(u_n) = (6.085, 6.5, 6.842, 7.058, ...)$ est une suite approximant, en milliards d'habitants, la population mondiale à partir de l'an 2000
 Dans les exemples précédents, on a $p_0 = 1; p_1 = 2, etc.$ et $u_0 = 6.085, u_1 = 6.5, etc. $. Sauf mention contraire, en général, le premier terme d'une suite est en fait le \"0-ème\" terme. Une suite peut être exprimée de manière explicite, c'est à l'aide d'une formule exacte permettant de calculer ses valeurs comme pour une fonction. Soit la suite $(u_n)$ définie explicitement par : $$ u_n = 2 n + 1$$ Alors, $u_0 = 1 ; u_1 = 3 ; u_2 = 5 ; ... ; u_{1000} = 2001 $; etc. (Il s'agit de la suite des nombres impairs). Une suite peut être exprimer de manière récursive, c'est à dire en exprimant le terme à venir $u_{n+1}$ par rapport au terme en cours $u_n$. Il n'est possible de calculer les termes de la suite qu'en commençant par le premier et en en déduisant ses successeurs les uns après les autres. Soit la suite $(u_n)$ définie récursivement par : $$ \begin{array}{lll} u_{n+1} &=& u_n + 2 \\ u_0 &=& 1 \end{array} $$ Alors, $u_0 = 1 ; u_1 = 3 ; u_2 = 5 $; etc. (Il s'agit de la même suite des nombres impairs).
  • La formule explicite d'une suite est pratique et permet de calculer directement n'importe quel terme, même d'indice grand
  • La formule récursive d'une suite ne permet pas de calculer directement n'importe quel terme. Son intérêt est plutôt descriptif. Dans l'exemple précédent, on comprend que $(u_n)$ est la suite qui démarre à 1 et ajouter 2 à chaque pas.
  • Une suite numérique peut très bien avoir une formule explicite et une formule récursive.
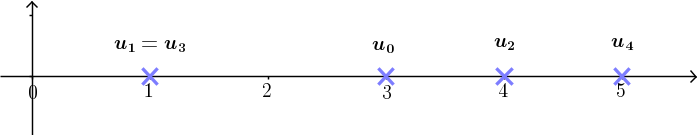
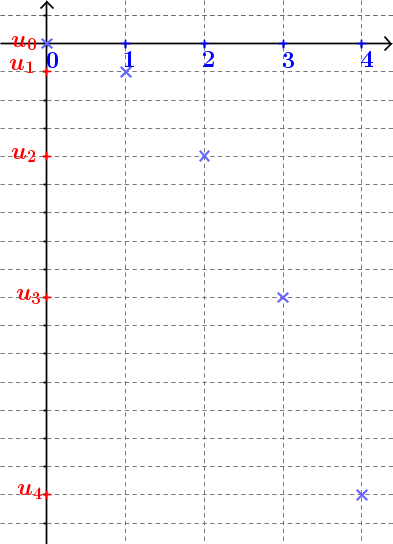
Représenter une suite numérique se fait simplement en plaçant les valeurs sur un axe. Il s'agit d'une représentation unidimentionnelle. On représente les premiers termes de la suite des décimales du nombre $\pi$ : Lorsque l'on utilise une fonction pour calculer les termes de la suite, il est possible d'utiliser un repère orthonormé du plan. Dans ce cas les termes de la suites se placent sur l'axe des abscisses et/ou des ordonnées Soit $(u_n)$ une suite définie explicitement pour tout $n \geq 0$ par : $$ u_n = f (n) $$ Pour tracer une valeur $u_k$ de la suite sur l'axe des ordonnées :
  • On lit la valeur $k$ sur l'axe des abscisses
  • On lit son image sur l'axe des ordonnées à l'aide de la courbe
  • Cette valeur est $u_k$
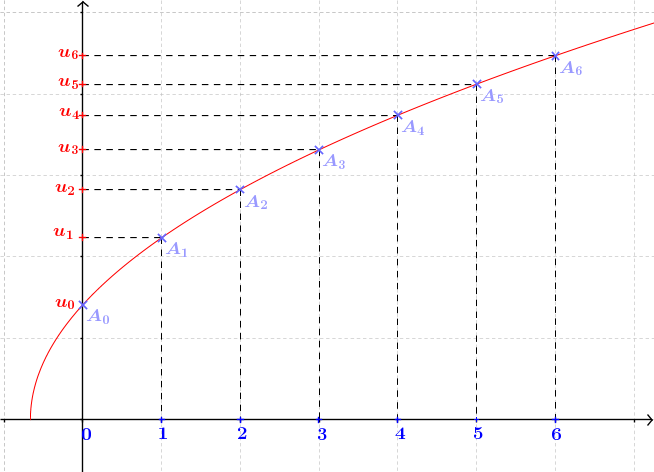
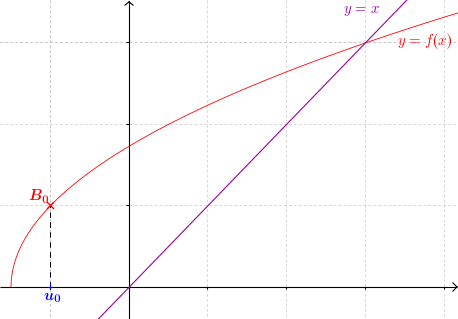
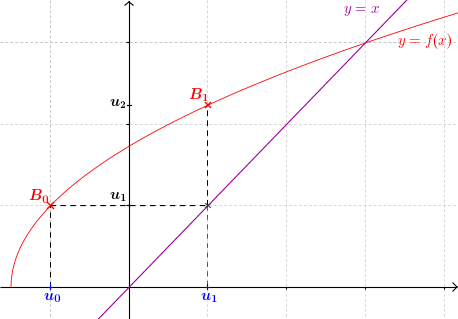
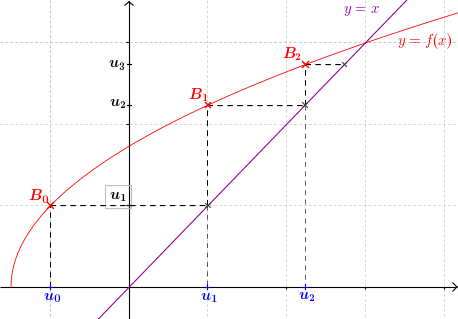
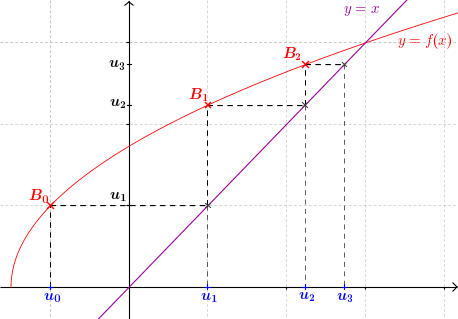
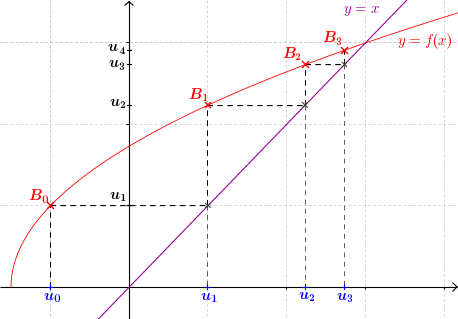
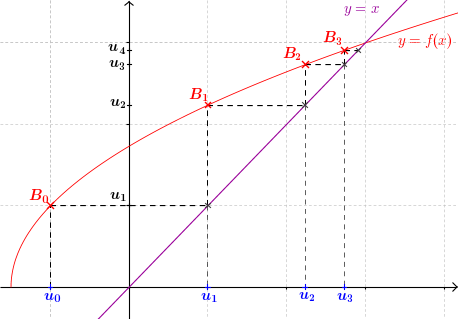
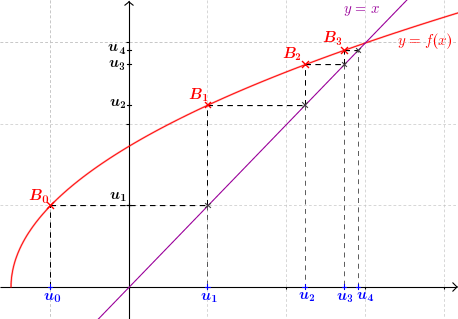
 Soit $(u_n)$ une suite définie récursivement pour tout $n \geq 0$ par : $$ \left\{ \begin{array}{lll} u_{n+1} &=& f (u_n) \\ u_0 &=& \text{valeur initiale} \end{array} \right. $$ On trace les valeurs les unes après les autres en partant de la première :
  • On place la valeur $u_0$ sur l'axe des abscisses
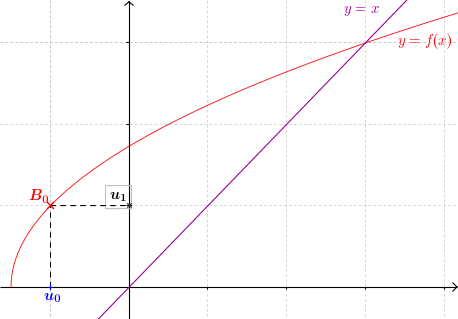
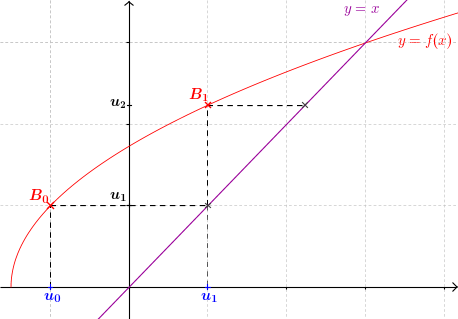
  • On lit son image sur l'axe des ordonnées à l'aide de la courbe. Il s'agit de $u_1 = f (u_0)$
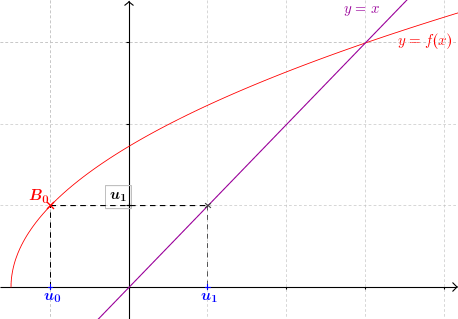
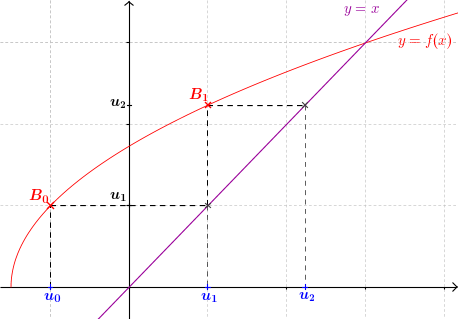
  • On reporte $u_1$ sur l'axe des abscisses à l'aide de la droite $y=x$
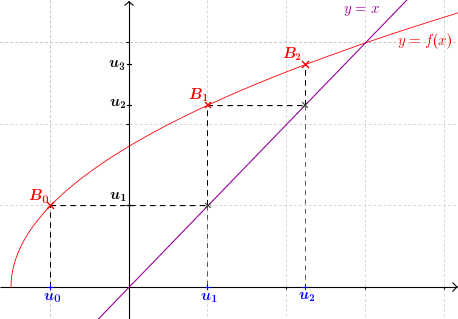
  • On répète les mêmes opérations à partir de $u_1$ pour obtenir $u_2$, etc.
  • Une suite $(u_n)$ est croissante à partir du rang $p$ si pour tout $n \geq p$ : $$ u_{n+1} \geq u_n $$
  • Une suite $(u_n)$ est décroissante à partir du rang $p$ si pour tout $n \geq p$ : $$ u_{n+1} \leq u_n $$
  • Une suite qui ne varie plus à partir du rang $p$ est dite stationnaire à partir du rang $p$
 Pour étudier les variations d'une suite $(u_n)$, on étudie le signe de la différence $u_{n+1} - u_n$ :
  • Si $u_{n+1} - u_n \geq 0$ pour tout $n \geq p$, la suite est croissante à partir du rang $p$.
  • Si $u_{n+1} - u_n \leq 0$ pour tout $n \geq p$, la suite est décroissante à partir du rang $p$.
Soit $(u_n)$ la suite définie explicitement par $u_{n} = n^2 + n$ pour tout $n \in \mathbb{N}$. On étudie le signe de $u_{n+1} - u_n$ : $$ \begin{array}{lll} & & u_{n+1} - u_n \\ &=& n^2 + n - n \\ &=& n^2 \geq 0 \end{array} $$ Donc la suite $(u_n)$ est croissante à partir du rang $0$. Soit $(u_n)$ la suite définie récursivement par $u_{n+1} = u_{n} - n$ pour tout $n \in \mathbb{N}$. On étudie le signe de $u_{n+1} - u_n$ : $$ \begin{array}{lll} & & u_{n+1} - u_n \\ &=& u_n - n - u_n \\ &=& - n \leq 0 \end{array} $$ Donc la suite $(u_n)$ est décroissante à partir du rang $0$. Dans certains cas, une propriété simple permet de déterminer les variations de la suite : Soit $(u_n)$ la suite définie explicitement par $u_{n} = f (n)$ pour tout $n \geq p$ où $f$ est une fonction croissante sur $[p;+\infty[$.

Alors la suite $(u_n)$ est croissante à partir du rang $p$

 Soit $(u_n)$ la suite définie explicitement par $u_{n} = \sqrt{n}$. Comme la fonction racine carré est croissante sur $[0;+\infty[$, la suite $(u_n)$ est croissante à partir du rang 0.
Pour comprendre l'idée de limite d'une suite, partons de l'exemple de la tortue : Une tortueLe paradoxe de Zénon où de "Achille et la tortue" est une histoire similaire dans laquelle Achille et une tortue font la course... Nous avons retiré Achille de l'histoire dont la présence en tant que "guest star" mythologique n'avait finalement que peu d'intérêt pour mettre en valeur la notion de limite. Pour les curieux, allez lire l'histoire sur wikipedia affamée et particulièrement faible se trouve à $1$ mètre d'une laitue appétissante. Elle est si fatiguée qu'elle doit marquer une pause chaque minute pour avancer vers l'objet de sa convoitise. Malheureusement l'effort est si intense que son énergie diminue à chaque effort, et la tortue n'arrive qu'à réaliser la moitié de la distance parcourue précédemment.

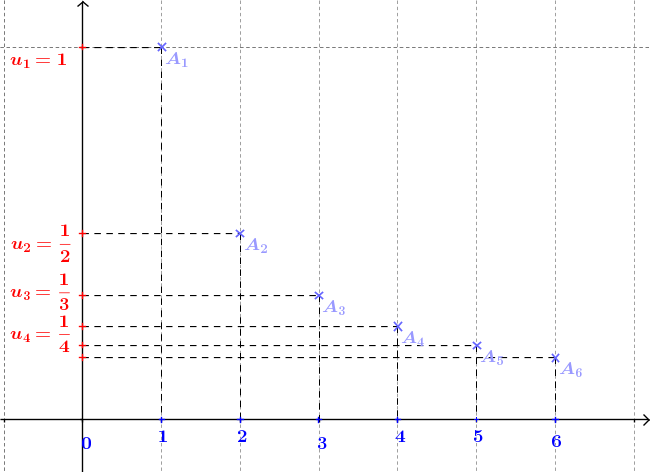
Ainsi, la tortue commence par parcourir la moitié de la distance totale ($0,5$ mètre), puis ajoute un quart ($0,75$ mètre), puis un huitième ($0,875$ mètre), puis un seizième ($0,9375$ mètre), etc.

On remarque plusieurs chose :

Traduisons ces remarques en termes de suites. On note $u_n$ la distance totale parcourue au bout de $n$ efforts ($u_0 = 0$, $u_1 = 0,5$, $u_2 = 0,75$, ... ) :

Attention, la limite de la suite n'est pas forcément une valeur de la suite. Une suite $(u_n)$ est convergente vers $\mathcal{l}$ si quand $n$ grandit à l'infini, les termes $u_n$ finissent par s'accumuler autour de $\mathcal{l}$. On note : $$ \lim_{n \mapsto +\infty} u_n = \mathcal{l} $$ Soit $(u_n)$ définie explicitement par $u_n = \frac{1}{n}$ pour tout $n \geq 1$ : $$ \lim_{n \mapsto +\infty} u_n = 0 $$ Une suite qui ne converge pas est divergente.
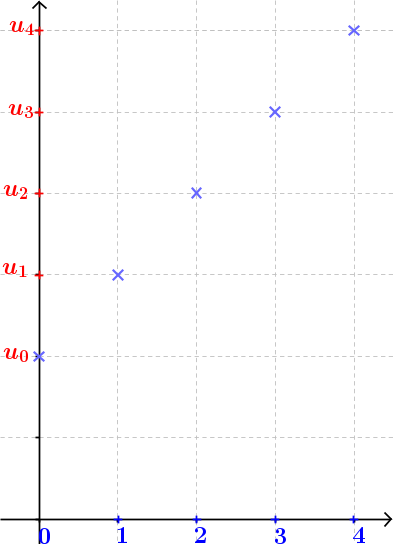
  • Si les valeurs de la suite sont de plus en plus grandes et ne sont pas majorée, on dit que $u_n$ tend vers $+\infty$
  • Si les valeurs de la suite sont de plus en plus grandes négativement et ne sont pas minorée, on dit que $u_n$ tend vers $-\infty$
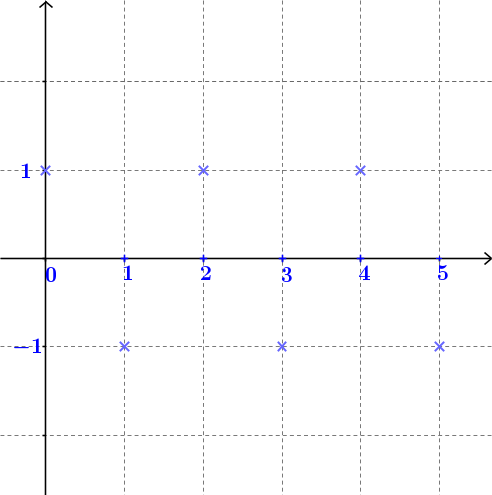
 Trois suites divergentes représentées avec un nuage de point :
$u_n = n + 2$ pour tout $n \geq 0$ : $v_n = -n^2$ pour tout $n \geq 0$ : $w_n = (-1)^n$ pour tout $n \geq 0$.
$$ \lim_{n \mapsto +\infty} u_n = +\infty $$ $$ \lim_{n \mapsto +\infty} v_n = -\infty $$

Alors la suite est divergente et n'admet pas de limite.
La suite définie récursivement par $u_0=1$ et $u_{n+1} = 1+\frac{1}{1+u_n}$ a pour limite $\sqrt{2}$. La notion de limite permet ainsi d'approcher des valeurs numériques.